Diffraction limits resolution.
The Rayleigh criterion states that two images are just resolvable when the centre of the diffraction pattern of one is directly over the first minimum of the diffraction pattern of the other.
Diffraction
Diffraction is the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture.
Single-slit diffraction
A long slit of infinitesimal width which is illuminated by light diffracts the light into a series of circular waves and the wavefront which emerges from the slit is a cylindrical wave of uniform intensity, in accordance with the Huygens–Fresnel principle.

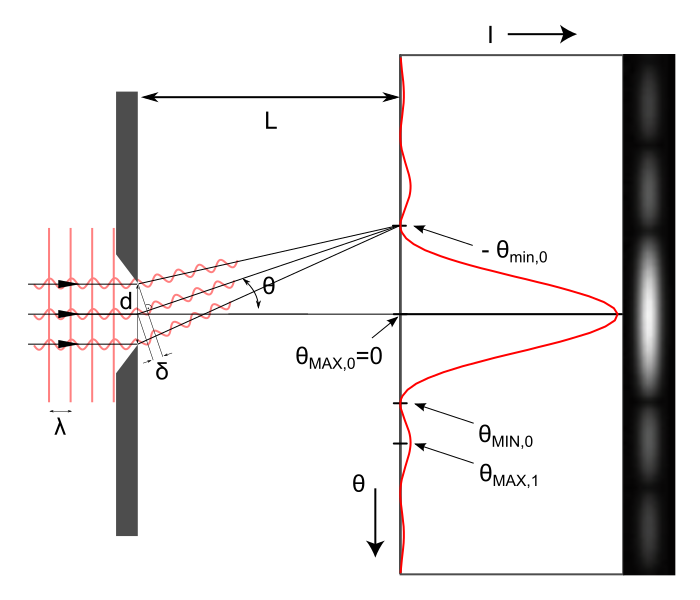
The far-field diffraction pattern of a plane wave incident on a circular aperture, known as the Airy disk, describes how the intensity of light varies with angle. The intensity distribution $I(\theta) as a function of the angle $\theta$ from the optical axis is given by:
$$
I(\theta) = I_0 \left(\frac{2J_1(k a \sin\theta)}{k a \sin\theta}\right)^2
$$
where $a$ is the radius of the circular aperture, $k$ is equal to $2\pi /\lambda $ and $J_{1}$ is a Bessel function. The smaller the aperture, the larger the spot size at a given distance, and the greater the divergence of the diffracted beams.
Resolution
Light diffracts as it moves through space, bending around obstacles, interfering constructively and destructively. Diffraction limits the detail we can obtain in images. The figure below shows the effect of passing light through a small circular aperture. Instead of a bright spot with sharp edges, a spot with a fuzzy edge surrounded by circles of light is obtained. This pattern is caused by diffraction similar to that produced by a single slit. Light from different parts of the circular aperture interferes constructively and destructively. The effect is most noticeable when the aperture is small, but the effect is there for large apertures, too.

Figure 3: Airy diffraction patterns generated by light from two point sources passing through a circular aperture. Points far apart (top) or meeting the Rayleigh criterion (middle) can be distinguished. Points closer than the Rayleigh criterion (bottom) are difficult to distinguish.
Figure 3(b) shows the diffraction pattern produced by two point light sources that are close to one another. The pattern is similar to that for a single point source, and it is just barely possible to tell that there are two light sources rather than one. If they were closer together, as in Figure 3(c), we could not distinguish them, thus limiting the detail or resolution we can obtain. This limit is an inescapable consequence of the wave nature of light. Thus light passing through a lens with a diameter D shows this effect and spreads, blurring the image, just as light passing through an aperture of diameter D does. So diffraction limits the resolution of any system having a lens or mirror. Telescopes are also limited by diffraction, because of the finite diameter D of their primary mirror.
The Rayleigh criterion
The imaging system’s resolution can be limited either by diffraction causing blurring of the image. Diffraction is determined by the finite aperture of the optical elements.
consider the diffraction pattern for a circular aperture, which has a central maximum that is wider and brighter than the maxima surrounding it (similar to a slit) [see Figure 4(a)]. It can be shown that, for a circular aperture of diameter D, the first minimum in the diffraction pattern occurs at $\theta = 1.22 {\lambda}/D$ (providing the aperture is large compared with the wavelength of light, which is the case for most optical instruments). The Rayleigh criterion for the diffraction limit to resolution states that two images are just resolvable when the centre of the diffraction pattern of one is directly over the first minimum of the diffraction pattern of the other. See Figure 4(b). The first minimum is at an angle of $\theta = 1.22 {\lambda}/D$, so that two point objects are just resolvable if they are separated by the angle
$$
\theta_{\text{min}} \approx \frac{1.22\lambda}{D}
$$
where $\lambda$ is the wavelength of light (or other electromagnetic radiation) and D is the diameter of the aperture, with which the two objects are observed. In this expression, $\theta$ has units of radians.
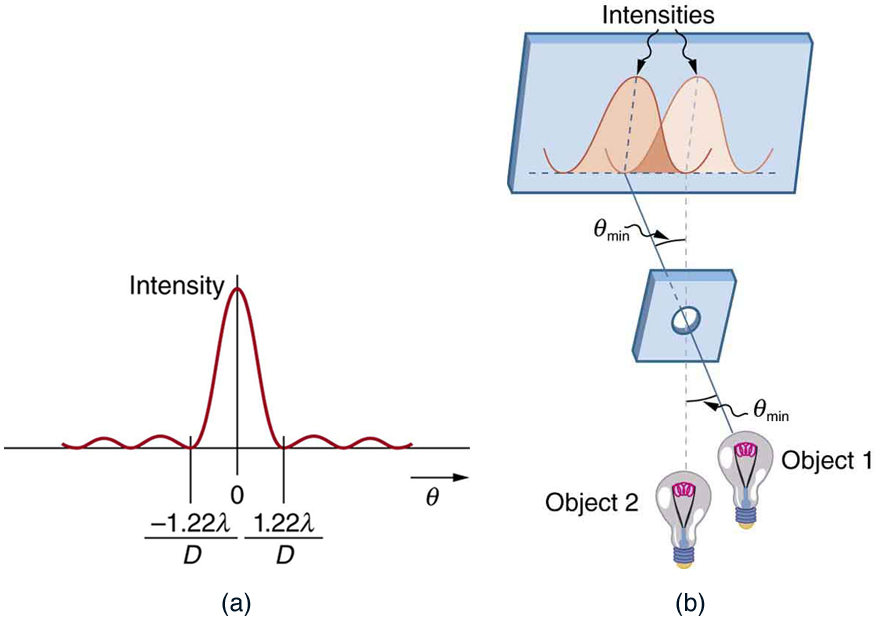
Figure 4: (a) Note that, similar to a single slit, the central maximum is wider and brighter than those to the sides. (b) Two point objects produce overlapping diffraction patterns. Shown here is the Rayleigh criterion for being just resolvable. The central maximum of one pattern lies on the first minimum of the other.
Factors Affecting α Value:
In the actual resolution calculation, as shown in the following equation. There exists a correction factor. This correction factor depends mainly on two factors, namely Illumination Distribution and Weighting Scheme.
$$
\theta \approx \alpha *\frac{\lambda}{D}
$$
Illumination Distribution
Illumination distribution refers to how the intensity of the signal is distributed across the aperture or array. It dictates the relative contribution of each part of the aperture to the final signal.
Uniform Illumination: Equal intensity across the entire aperture, which can result in high side lobes. Uniform Illumination: Results in an $\alpha$ value close to 1, such as 1.02 for a uniformly illuminated circular aperture. It provides a narrower main lobe but higher side lobes.
Tapered Illumination: Intensity decreases towards the edges, which reduces side lobes but can widen the main lobe. Tapered Illumination: Involves decreasing illumination towards the edges, resulting in a higher $\alpha$ value (e.g., between 1.2 and 1.5). This helps in reducing side lobes but can widen the main lobe.
Natural Illumination: Adjusted based on practical needs or conditions, providing a balance between performance metrics.
Weighting Scheme
Definition refers to the relative gain or importance assigned to different elements or signal sources. It determines how much each component contributes to the final result.
Uniform Weighting: All elements or signals are assigned equal weights. This often results in an $\alpha$ value lower than 1, such as 0.8, indicating improved resolution but potentially higher side lobes.
Tapered Weighting: Weight decreases towards the edges, reducing side lobes but potentially increasing the main lobe width.
Natural Weighting: Adjusts weights based on signal needs or conditions, usually maintaining an $\alpha$ value close to 1.0.
Adaptive Weighting: Dynamically adjusts weights based on real-time data, optimizing performance in varying conditions, affecting the $\alpha$ value accordingly..


